प्रस्तावना –
भारतीय संख्या प्रणाली, जिसे हिंदू-अरबी अंक प्रणाली के रूप में भी जाना जाता है, एक अंक प्रणाली है जो शून्य से नौ तक की संख्या का प्रतिनिधित्व करने के लिए दस प्रतीकों का उपयोग करती है। यह प्रणाली भारत और दुनिया भर में व्यापक रूप से उपयोग की जाती है, और इसे सबसे कुशल और बहुमुखी अंक प्रणालियों में से एक माना जाता है। भारतीय संख्या प्रणाली भारत में 500 ईसा पूर्व के आसपास उत्पन्न हुई थी, और इसे बाद में अरबों द्वारा अपनाया गया और आगे विकसित किया गया। यह एक दशमलव प्रणाली का उपयोग करता है, जिसका अर्थ है कि किसी अंक का मान संख्या में उसकी स्थिति से निर्धारित होता है।

';
}
else
{
echo "Sorry! You are Blocked from seeing the Ads";
}
?>
उदाहरण के लिए, संख्या 123 में, अंक 3 इकाई स्थान का प्रतिनिधित्व करता है, अंक 2 दहाई स्थान का प्रतिनिधित्व करता है, और अंक 1 सौ स्थान का प्रतिनिधित्व करता है। भारतीय संख्या प्रणाली में प्रयुक्त दस प्रतीकों को अंकों के रूप में जाना जाता है, और वे हैं: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 इन अंकों को किसी भी संख्या का प्रतिनिधित्व करने के लिए जोड़ा जा सकता है, चाहे वह कितना भी बड़ा या छोटा क्यों न हो। उदाहरण के लिए, इन दस प्रतीकों का उपयोग करके संख्या 123,456,789 लिखी जा सकती है।

भारतीय संख्या प्रणाली के प्रमुख लाभों में से एक इसकी सरलता और उपयोग में आसानी है। सिस्टम को सीखना और समझना आसान है, और यह कुशल गणना और गणितीय संचालन की अनुमति देता है। इसके अलावा, स्थानीय मान का उपयोग अपेक्षाकृत कम संख्या में प्रतीकों का उपयोग करके बड़ी संख्या का प्रतिनिधित्व करने की अनुमति देता है। कुल मिलाकर, भारतीय संख्या प्रणाली गणित का एक मूलभूत हिस्सा है और इसका दुनिया भर में विज्ञान, प्रौद्योगिकी और वाणिज्य के विकास पर महत्वपूर्ण प्रभाव पड़ा है।
वैदिक ग्रंथो में अंक प्रणाली –
वैदिक संख्या प्रणाली एक प्राचीन अंक प्रणाली है जिसका उपयोग भारत में वैदिक काल के दौरान किया गया था, जो लगभग 1500-500 ईसा पूर्व की है। इस प्रणाली का उपयोग वेदों के पवित्र ग्रंथों में किया गया था, जिसमें ऋग्वेद, यजुर्वेद, सामवेद और अथर्ववेद शामिल हैं। वैदिक संख्या प्रणाली दशमलव और विजीसिमल प्रणालियों के संयोजन पर आधारित है, जिसका अर्थ है कि यह आधार 10 और आधार 20 दोनों का उपयोग करता है। वैदिक संख्या प्रणाली संख्याओं का प्रतिनिधित्व करने के लिए प्रतीकों के एक सेट का उपयोग करती है। प्रतीकों को “अक्षर” या “वर्ण” कहा जाता है, जिसका अर्थ है “अक्षर” या “ध्वनियाँ।” वैदिक संख्या प्रणाली में 54 अक्षर हैं, जिन्हें प्रत्येक 18 के तीन समूहों में विभाजित किया गया है।
पहला समूह इकाइयों का प्रतिनिधित्व करता है, दूसरा समूह दसियों का प्रतिनिधित्व करता है और तीसरा समूह सैकड़ों का प्रतिनिधित्व करता है। वैदिक संख्या प्रणाली में, प्रत्येक संख्या को इन अक्षरों के संयोजन के रूप में व्यक्त किया जाता है। उदाहरण के लिए, संख्या 123 को “एक-शता-द्वि-दास” के रूप में व्यक्त किया गया है, जिसका अर्थ है “एक सौ दो दस और तीन।” वैदिक संख्या प्रणाली में अंकगणितीय संक्रियाओं को करने के लिए गणितीय नियमों का एक समूह भी शामिल है।
इन नियमों को “सूत्र” के रूप में जाना जाता है, जिसका अर्थ है “सूत्र” या “धागे”। सूत्र लिखित गणना की आवश्यकता के बिना, मानसिक रूप से गणना करने के लिए दिशा-निर्देशों का एक सेट प्रदान करते हैं। सबसे प्रसिद्ध सूत्रों में से एक “वैदिक गुणन सूत्र” है, जो एक पंक्ति में दो संख्याओं के गुणन की अनुमति देता है। यह सूत्र “ऊर्ध्वाधर और आड़े-तिरछे” गुणन के विचार पर आधारित है, जहाँ प्रत्येक स्थान के मान में अंकों के गुणनफल की गणना की जाती है और फिर अंतिम परिणाम प्राप्त करने के लिए एक साथ जोड़ा जाता है। कुल मिलाकर, वैदिक संख्या प्रणाली भारतीय गणित का एक महत्वपूर्ण हिस्सा है और इसका भारत और दुनिया भर में गणितीय ज्ञान और तकनीकों के विकास पर महत्वपूर्ण प्रभाव पड़ा है।
ब्राम्हण ग्रंथों में अंक प्रणाली –
ब्राह्मण साहित्य में संख्या प्रणाली प्राचीन धार्मिक ग्रंथों में प्रयुक्त संख्या प्रणाली को संदर्भित करती है, जिन्हें ब्राह्मण कहा जाता है, जो वैदिक साहित्य का हिस्सा हैं। ब्राह्मण वैदिक संस्कृत में लिखे गए थे, और वे लगभग 1000-800 ईसा पूर्व के हैं। ब्राह्मणों में प्रयुक्त अंक प्रणाली वैदिक संख्या प्रणाली के समान दशमलव और विगेजिमल प्रणालियों के संयोजन पर आधारित है। प्रणाली संख्याओं का प्रतिनिधित्व करने के लिए प्रतीकों के एक सेट का उपयोग करती है, जो संस्कृत भाषा पर आधारित हैं। ब्राह्मण संख्या प्रणाली में प्रयुक्त प्रतीकों को “अक्षर” या “वर्ण” भी कहा जाता है, जिसका अर्थ है “अक्षर” या “ध्वनियाँ”। ब्राह्मण संख्या प्रणाली संख्याओं का प्रतिनिधित्व करने के लिए 42 अक्षरों के एक सेट का उपयोग करती है, जिन्हें प्रत्येक 14 के तीन समूहों में विभाजित किया जाता है। पहला समूह इकाइयों का प्रतिनिधित्व करता है, दूसरा समूह दसियों का प्रतिनिधित्व करता है और तीसरा समूह सैकड़ों का प्रतिनिधित्व करता है।
ब्राह्मणों में अंकगणितीय संक्रियाओं को करने के लिए गणितीय नियम भी शामिल हैं, जो वैदिक सूत्रों के समान हैं। ब्राह्मण संख्या प्रणाली की उल्लेखनीय विशेषताओं में से एक अनंत की अवधारणा का उपयोग है। ब्राह्मण अनंत को “अनंत” कहते हैं, जिसका अर्थ है “अंतहीन” या “अनंत”। ब्रह्मांड और परमात्मा की असीम प्रकृति का प्रतिनिधित्व करने के लिए अनंतता की अवधारणा का प्रतीकात्मक अर्थ में उपयोग किया जाता है। ब्राह्मण संख्या प्रणाली में संख्याओं का प्रतिनिधित्व करने के लिए ज्यामितीय आकृतियों का उपयोग भी शामिल है। उदाहरण के लिए, संख्या 4 का प्रतिनिधित्व करने के लिए एक वर्ग का उपयोग किया जाता है, और संख्या 1 का प्रतिनिधित्व करने के लिए एक वृत्त का उपयोग किया जाता है। संख्याओं का प्रतिनिधित्व करने के लिए ज्यामितीय आकृतियों का उपयोग करने की इस प्रणाली को “यंत्र” कहा जाता है, जिसका अर्थ है “यंत्र” या “मशीन”।
बौध्द एवं जैन ग्रंथों में अंक प्रणाली ––
बौद्ध साहित्य में संख्या प्रणाली प्राचीन बौद्ध ग्रंथों में प्रयुक्त अंक प्रणाली को संदर्भित करती है, जिसमें पाली कैनन और त्रिपिटक शामिल हैं। बौद्ध ग्रंथ पाली और संस्कृत सहित विभिन्न प्राचीन भाषाओं में लिखे गए थे, और वे लगभग 500 ईसा पूर्व के हैं। बौद्ध साहित्य में प्रयुक्त अंक प्रणाली दशमलव प्रणाली पर आधारित है, जिसका अर्थ है कि यह शून्य से नौ तक की संख्याओं को दर्शाने के लिए दस प्रतीकों का उपयोग करती है। सिस्टम संख्याओं का प्रतिनिधित्व करने के लिए प्रतीकों के एक सेट का उपयोग करता है, जो पाठ की भाषा पर आधारित होते हैं। बौद्ध संख्या प्रणाली में प्रयुक्त प्रतीकों को “अक्षर” या “वर्ण” भी कहा जाता है, जिसका अर्थ है “अक्षर” या “ध्वनियाँ”। बौद्ध संख्या प्रणाली संख्याओं का प्रतिनिधित्व करने के लिए 10 अक्षरों के एक सेट का उपयोग करती है, जो बाएं से दाएं लिखी जाती हैं। किसी अंक का मान संख्या में उसकी स्थिति से निर्धारित होता है।
जैन संख्या प्रणाली में अंकगणितीय संक्रियाओं को करने के लिए गणितीय नियम भी शामिल हैं। ये नियम अन्य प्राचीन भारतीय संख्या प्रणालियों में प्रयुक्त गणितीय नियमों के समान हैं। जैन संख्या प्रणाली की उल्लेखनीय विशेषताओं में से एक शून्य का प्रतिनिधित्व करने के लिए एक विशेष प्रतीक का उपयोग है। शून्य का प्रतीक एक बिंदु है, जो एक अंक की अनुपस्थिति को इंगित करने के लिए एक संख्या में उपयुक्त स्थिति में रखा जाता है। शून्य का उपयोग गणित में एक महत्वपूर्ण विकास था, और इसने आधुनिक अंकगणित और बीजगणित के विकास का मार्ग प्रशस्त किया। कुल मिलाकर, जैन अंक प्रणाली प्राचीन भारतीय गणित का एक महत्वपूर्ण हिस्सा है और इसका भारत और दुनिया भर में गणितीय ज्ञान और तकनीकों के विकास पर महत्वपूर्ण प्रभाव पड़ा है। जैन ग्रंथों में शून्य और दशमलव प्रणाली के उपयोग ने आधुनिक गणित के विकास और विज्ञान और प्रौद्योगिकी में इसके अनुप्रयोगों की नींव रखी।
उदाहरण के लिए, संख्या 123 में, अंक 3 इकाई स्थान का प्रतिनिधित्व करता है, अंक 2 दहाई स्थान का प्रतिनिधित्व करता है, और अंक 1 सौ स्थान का प्रतिनिधित्व करता है। बौद्ध संख्या प्रणाली में अंकगणितीय संक्रियाओं को करने के लिए गणितीय नियम भी शामिल हैं। ये नियम जोड़, घटाव, गुणा और भाग के सिद्धांतों पर आधारित हैं। शून्य की अवधारणा का उपयोग बौद्ध संख्या प्रणाली की उल्लेखनीय विशेषताओं में से एक है। शून्य की अवधारणा का उपयोग बौद्ध ग्रंथों में मात्रा या मूल्य की अनुपस्थिति को दर्शाने के लिए किया जाता है। शून्य का उपयोग गणित में एक महत्वपूर्ण विकास था, और इसने आधुनिक अंकगणित और बीजगणित के विकास का मार्ग प्रशस्त किया। कुल मिलाकर, बौद्ध संख्या प्रणाली प्राचीन भारतीय गणित का एक महत्वपूर्ण हिस्सा है और इसका भारत और दुनिया भर में गणितीय ज्ञान और तकनीकों के विकास पर महत्वपूर्ण प्रभाव पड़ा है। बौद्ध ग्रंथों में शून्य और दशमलव प्रणाली के उपयोग ने आधुनिक गणित के विकास और विज्ञान और प्रौद्योगिकी में इसके अनुप्रयोगों की नींव रखी।
प्राचीन भारत में गणित की उत्पत्ति का पता सिंधु घाटी सभ्यता से लगाया जा सकता है, जो 2600 ईसा पूर्व से 1900 ईसा पूर्व तक अस्तित्व में थी। सिंधु घाटी सभ्यता अपनी उन्नत नगरीय योजना, व्यापार और कृषि के लिए जानी जाती थी और इस सभ्यता के लोग बाट और माप की एक परिष्कृत प्रणाली का उपयोग करते थे। गणितीय ज्ञान और तकनीकों का विकास वैदिक काल तक जारी रहा, जो लगभग 1500 ईसा पूर्व शुरू हुआ। वेद, जो प्राचीन हिंदू ग्रंथों का एक संग्रह है, में गणितीय अवधारणाओं जैसे कि गिनती, ज्यामिति और बीजगणित के संदर्भ शामिल हैं। वैदिक काल में दशमलव प्रणाली का विकास भी देखा गया, जो दस अंकों के उपयोग पर आधारित है।
400 ईसा पूर्व से 200 सीई तक की अवधि, जिसे “भारत का स्वर्ण युग” कहा जाता है, गणित में महत्वपूर्ण प्रगति का समय था। इस अवधि के दौरान, गणितज्ञों ने ज्यामिति, बीजगणित और त्रिकोणमिति के क्षेत्र में महत्वपूर्ण योगदान दिया। गणितज्ञ आर्यभट्ट, जो 5वीं शताब्दी सीई में रहते थे, को शून्य की अवधारणा को विकसित करने और बीजगणित और त्रिकोणमिति में महत्वपूर्ण प्रगति करने का श्रेय दिया जाता है। प्राचीन भारत के एक अन्य महत्वपूर्ण गणितज्ञ ब्रह्मगुप्त थे, जो 7वीं शताब्दी ईस्वी में रहते थे। उन्होंने बीजगणित और संख्या सिद्धांत के क्षेत्र में महत्वपूर्ण योगदान दिया, और उन्हें द्विघात समीकरणों को हल करने के लिए नियम विकसित करने का श्रेय दिया जाता है। प्राचीन भारत में विकसित गणितीय ज्ञान और तकनीकों का दुनिया भर में गणित और विज्ञान के विकास पर महत्वपूर्ण प्रभाव पड़ा। दशमलव प्रणाली, जिसे भारत में विकसित किया गया था, अब दुनिया के अधिकांश हिस्सों में उपयोग की जाती है, और शून्य की अवधारणा का गणित और विज्ञान पर गहरा प्रभाव पड़ा है। प्राचीन भारतीय गणितज्ञों के काम ने आधुनिक गणित के विकास और विज्ञान और प्रौद्योगिकी में इसके अनुप्रयोगों की नींव रखी।
भारत में गणित की उत्पत्ति एवं विकास –
भारत में गणित का एक लंबा और समृद्ध इतिहास है, प्राचीन काल से जब भारतीय गणितज्ञों ने इस क्षेत्र में महत्वपूर्ण योगदान दिया था। गणित के आक्रमण ने भारत के विकास में एक महत्वपूर्ण भूमिका निभाई है, और यह कई क्षेत्रों में प्रगति और नवाचार को चलाने के लिए एक महत्वपूर्ण उपकरण बना हुआ है। एक क्षेत्र जहां भारत के विकास में गणित आवश्यक रहा है वह है विज्ञान और प्रौद्योगिकी। भारत में एक संपन्न तकनीकी उद्योग है, और गणित इसके कई नवाचारों के मूल में है। भारतीय गणितज्ञों ने कंप्यूटर विज्ञान और सूचना प्रौद्योगिकी के विकास में महत्वपूर्ण योगदान दिया है, और भारत की कई शीर्ष तकनीकी कंपनियां एल्गोरिदम, डेटा संरचनाओं और अनुकूलन तकनीकों जैसी गणितीय अवधारणाओं पर भरोसा करती हैं। भारत के अंतरिक्ष कार्यक्रम के विकास में गणित का भी महत्वपूर्ण योगदान रहा है। भारतीय गणितज्ञों ने अंतरिक्ष यान प्रक्षेपवक्र योजना और कक्षीय यांत्रिकी के लिए एल्गोरिदम के विकास में महत्वपूर्ण योगदान दिया है। भारतीय अंतरिक्ष अनुसंधान संगठन (इसरो) गणितीय सिद्धांतों के अनुप्रयोग के कारण अंतरिक्ष में कई सफल मिशन लॉन्च करने में सक्षम रहा है।
गणितीय विकास की ऐतिहासिक पृष्ठभूमि –
प्राचीन भारत में गणित का एक लंबा और समृद्ध इतिहास है, जो लगभग 3000 ईसा पूर्व सिंधु घाटी सभ्यता से जुड़ा है। भारत में गणितीय ज्ञान का सबसे पहला प्रमाण हड़प्पा संस्कृति में पाया जा सकता है, जहां व्यापार और वाणिज्य में शासक, तराजू और बाट जैसे उपकरणों का उपयोग किया जाता था।
भारत में सबसे पहले दर्ज किए गए गणितीय ग्रंथ सुल्वसूत्र हैं, जो लगभग 800 ईसा पूर्व वैदिक संस्कृत में लिखे गए थे। इन ग्रंथों में वैदिक अनुष्ठानों के लिए वेदियों और अग्निकुंडों के निर्माण के नियम और सूत्र हैं, और वे ज्यामिति, बीजगणित और अंकगणित के उन्नत ज्ञान को दर्शाते हैं। सुल्वसूत्र में प्रसिद्ध पायथागॉरियन प्रमेय शामिल है, जो प्राचीन ग्रीस में खोजे जाने से कई शताब्दियों पहले भारत में जाना जाता था। सबसे प्रभावशाली प्राचीन भारतीय गणितज्ञों में से एक आर्यभट्ट थे, जो 5वीं शताब्दी सीई में रहते थे। आर्यभट को शून्य और दशमलव संख्या प्रणाली की अवधारणा विकसित करने का श्रेय दिया जाता है, जो बाद में अरब दुनिया और यूरोप में प्रसारित हुए। उन्होंने बीजगणित, त्रिकोणमिति और खगोल विज्ञान में भी महत्वपूर्ण योगदान दिया।भास्कराचार्य ने ‘ लीलावती” तथा आर्यभट्ट ने ‘आर्यभट्टीयम’ में अंक गणित, रेखागणित और बीजगणित के सिद्धांत प्रतिपादित किए। आर्यभट्ट ने वृत्त के क्षेत्रफल का सिद्धांत भी दिया जिसमें उन्होंने कहा कि यह परिधि तथा व्यास के आधे का गुणनफल 1/2 परिधि x 1/2 व्यास होता है। एक अन्य प्रभावशाली प्राचीन भारतीय गणितज्ञ ब्रह्मगुप्त थे, जो 7वीं शताब्दी ई.पू. में रहते थे। इन्होंने ‘ ब्रम्हास्फुट सिद्धांत’ वृत्तीय चतुर्भुज का क्षेत्रफल, ‘सूची स्तम्भ’ , छिन्नक (Frustum) संबंधी सिद्धांतों के प्रसिद्ध सिद्धांत है। भास्कराचार्य ने ‘बीजगणित’ में धनर्णसंख्याओं के योग, करणी संख्याओं के योग, भाजक तथा भाज्य की प्रक्रिया, वर्ग प्रकृति, अनेक समीकरणों जैसे विषयों पर नियम लिखे।
ब्रह्मगुप्त बीजगणितीय समीकरणों, द्विघात समीकरणों और अनिश्चित समीकरणों के समाधान पर अपने काम के लिए जाने जाते हैं। उन्होंने खगोल विज्ञान के अध्ययन में भी महत्वपूर्ण योगदान दिया और ऋणात्मक संख्याओं का पहला व्यवस्थित उपचार प्रदान किया। इन गणितज्ञों के अलावा, प्राचीन भारत में और भी कई लोग थे जिन्होंने इस क्षेत्र में महत्वपूर्ण योगदान दिया। प्राचीन भारत में गणित का आक्रमण विज्ञान, धर्म और दर्शन में एक मजबूत रुचि से प्रेरित था, और इसने भारतीय उपमहाद्वीप की बौद्धिक और सांस्कृतिक विरासत को आकार देने में महत्वपूर्ण भूमिका निभाई।
शून्य का आविष्कार –
शून्य की अवधारणा, जो गणित और विज्ञान में एक मौलिक अवधारणा है, प्राचीन भारत में खोजी गई थी। शून्य की खोज गणित के इतिहास में एक महत्वपूर्ण मील का पत्थर है और इसका आधुनिक गणित और विज्ञान के विकास पर गहरा प्रभाव पड़ा है। शून्य की अवधारणा का दशमलव प्रणाली के विकास से गहरा संबंध है, जो दस अंकों के उपयोग पर आधारित है। भारत में दशमलव प्रणाली का विकास वैदिक काल के दौरान हुआ था, जो लगभग 1500 ईसा पूर्व शुरू हुआ था। दस अंकों के उपयोग ने अंकगणितीय संक्रियाओं को करना आसान बना दिया, और इसने अधिक परिष्कृत गणितीय तकनीकों के विकास का मार्ग प्रशस्त किया।

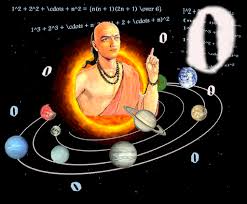
एक निर्धारक (placeholder) के रूप में शून्य का उपयोग पहली बार भारत में गणितज्ञ आर्यभट्ट द्वारा 5वीं शताब्दी सीई में विकसित किया गया था। आर्यभट ने शून्य का प्रतिनिधित्व करने के लिए एक प्रतीक का उपयोग किया, जो संख्याओं के नीचे एक बिंदु था।शून्य भारत में संख्या पद्धती का एक महत्वपूर्ण हिस्सा बन गया यहाँ तक कि पहले गणितीय समीकरणों को कविता के रूप में गाया जाता था। आकाश और अंतरिक्ष जैसे शब्द “कुछ भी नही” अर्थात शून्य का प्रतिनिधित्व करते हैं। यह प्रतीक बाद में अन्य भारतीय गणितज्ञों द्वारा अपनाया गया और शून्य के लिए मानक प्रतीक बन गया। शून्य की अवधारणा को दुनिया के अन्य हिस्सों में तुरंत स्वीकार नहीं किया गया था, और इसे व्यापक रूप से इस्तेमाल होने में कई शताब्दियां लग गईं। यूरोप में शून्य को अपनाने में इतालवी गणितज्ञ फाइबोनैचि के काम से मदद मिली, जिन्होंने 13वीं शताब्दी में यूरोप में हिंदू-अरबी अंक प्रणाली की शुरुआत की, जिसमें शून्य का उपयोग शामिल है।
शून्य की खोज का गणित और विज्ञान के विकास पर गहरा प्रभाव पड़ा। इसने अंकगणितीय संक्रियाओं को अधिक कुशलता से करना संभव बना दिया, और इसने बीजगणित और कलन जैसी अधिक परिष्कृत गणितीय तकनीकों के विकास का मार्ग प्रशस्त किया। शून्य की अवधारणा का विज्ञान के विकास पर भी महत्वपूर्ण प्रभाव पड़ा, विशेष रूप से भौतिकी और खगोल विज्ञान के क्षेत्र में, जहां इसका उपयोग मात्रा की अनुपस्थिति या शून्य मान का प्रतिनिधित्व करने के लिए किया जाता है।
निष्कर्ष –
अंत में, प्राचीन भारत ने दशमलव प्रणाली की खोज, बीजगणित और त्रिकोणमिति के विकास और शून्य की खोज सहित गणित के विकास में महत्वपूर्ण योगदान दिया। ये गणितीय प्रगति हजारों वर्षों की अवधि में की गई थी, जो सिंधु घाटी सभ्यता से शुरू हुई और वैदिक काल और “भारत के स्वर्ण युग” तक जारी रही। विशेष रूप से शून्य की खोज, गणित के इतिहास में एक महत्वपूर्ण मील का पत्थर थी और इसका आधुनिक गणित और विज्ञान के विकास पर गहरा प्रभाव पड़ा। एक प्लेसहोल्डर के रूप में शून्य के उपयोग ने अंकगणितीय संक्रियाओं को करना आसान बना दिया और बीजगणित और कलन जैसी अधिक परिष्कृत गणितीय तकनीकों के विकास का मार्ग प्रशस्त किया। शून्य की अवधारणा का विज्ञान के विकास पर महत्वपूर्ण प्रभाव पड़ा है, विशेष रूप से भौतिकी और खगोल विज्ञान के क्षेत्र में, जहाँ इसका उपयोग मात्रा की अनुपस्थिति या शून्य मान का प्रतिनिधित्व करने के लिए किया जाता है। प्राचीन भारतीय गणितज्ञों के काम ने आधुनिक गणित के विकास और विज्ञान और प्रौद्योगिकी में इसके अनुप्रयोगों की नींव रखी। इन गणितज्ञों द्वारा की गई खोजों ने आधुनिक गणित को प्रभावित करना जारी रखा है, और उनकी विरासत गणित और विज्ञान के इतिहास का एक महत्वपूर्ण हिस्सा है।
Post Views: 294
Like this:
Like Loading...
Related


